Este va a ser un buen año (de medusas)

Entendemos por ecuación una expresión en la que ligamos -mediante diversas operaciones matemáticas- variables y constantes con una relación de igualdad entre sus dos miembros.
Una ecuación en una, dos o más variables define una forma –que llamaremos gráfica- en un espacio de una, dos o más dimensiones.
La geometría analítica se ocupa entre otras de tales cuestiones.
Es práctica habitual la representación de figuras planas como la línea recta, circunferencia, parábola o hipérbola, asociadas a ecuaciones en x,y en un primer curso de bachillerato; incluso la representación de funciones periódicas –seno, coseno, etc.- se estudian en dicho nivel.
Por otra parte se reserva la geometría analítica en el espacio, en x,y,z, es decir con ecuaciones de tres variables o en un espacio de tres dimensiones, para un segundo nivel de bachillerato (antes llamado preuniversitario).

Supongamos una forma en dos dimensiones, como la parábola: la ecuación

y = x^2 - 3x + 5

determina la siguiente gráfica, lugar geométrico de todos los puntos del plano que satisfacen dicha ecuación.

Pero una vez trazada la parábola en realidad quedan definidas tres zonas: los puntos del plano que quedan sobre ella, ella misma y los puntos que se sitúan bajo dicha curva.
Tales regiones podemos identificarlas con las expresiones siguientes:

y > x^2 - 3x + 5
y = x^2 - 3x + 5
y < x^2 - 3x + 5

No vamos a detallar aquí que estas expresiones en las que se sustituye el signo de igualdad por la condición de mayor (>) o menor (<) se estudian bajo en nombre genérico de inecuaciones, ni tampoco sus propiedades e interesantes aplicaciones en la optimización de recursos –materia de la programación lineal- pero si que su manejo, más allá de su aspecto teórico o aplicaciones practicas en economía, permite generar imágenes, que -por lo insospechado de su aspecto- no parecen fruto del cálculo algebraico sino más bien producto de la mano de un artista.

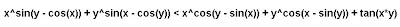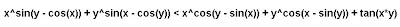Ayudados por un programa informático de representación gráfica nos podemos animar a escribir inecuaciones como... que divide el plano en regiones -de las que la propia curva queda incluida como borde de una de ellas- y coloreando adecuadamente por fin conseguimos estos biomorfos:

Grupo de medusas (Medusina cosinusina ssp tangentiana) nadando en libertad en el océano del plano.

Extensa colonia de medusas reproduciéndose por escisión de pólipos anclados al substrato -los ejes de coordenadas- de los que se separan por estrobilación.

Benoît Mandelbrot ya tuvo su oportunidad; ahora animo al lector a bajar este software y a probar suerte: el mar -como el plano- esta lleno de criaturas, muchas de ellas aun por descubrir.