Según la mitología griega uno de los doce trabajos que le fueron encomendados a Hércules consistió en derrotar a un monstruo con nueve cabezas de serpiente venenosas. Esta bestia estaba en una comarca alrededor del lago de Lerna, de ahí el nombre de la Hiedra de Lerna. Cuenta la historia que de inmediato que se le cortaba una cabeza regeneraba una nueva, Hércules logró vencerla quemando con una antorcha los cuellos cercenados para evitar que de ellos emergieran la nuevas cabezas.
También existe otra historia que cuenta el castigo que se le impuso a Prometeo por robar el fuego sagrado del Olimpo y regalárselo a los hombres. Fue condenado a permanecer encadenado en un alto pico de las montañas del Cáucaso para que un águila le devorara el hígado eternamente, pues Prometeo era inmortal y este órgano se regeneraba tan rápidamente como era devorado.
Ambas leyendas griegas muestran el conocimiento que ya tenían los antiguos sobre la capacidad de regeneración célular, aunque por supuesto, en la realidad no es tan espectacular como en las leyendas, las cuales representan un interesante vínculo entre los conocimientos científicos y la mitología.
La regeneración biológica o célular se define como la capacidad que poseen ciertos organismos vivos para restaurar un tejido perdido o lesionado o de hacer crecer nuevamente una parte de su cuerpo perdida por causa accidental, causada o fisiológica.
La primera observación que se tuvo sobre este acontecimiento fue en las plantas. Un conocimiento básico fue la observación de que muchos árboles podían ser cortados por el tronco al nivel de la tierra, pero podían posteriormente regenerarse completamente si sus raíces no se habían destruido. Observaciones como esta permitieron una extensa evolución en el campo de la botánica y la agricultura. En la actualidad, al concepto clásico de regeneración se puede adicionar el proceso de obtención de una planta a partir de una sola célula vegetal o de un grupo de ellas, lo que es avalado por las técnicas de avanzada que permiten generar plantas in vitro y modificar sus características.
La regeneración biológica se comporta de forma diferente en los distintos tipos de animales, pues mientras resulta común en los invertebrados, se encuentra limitada en la mayoría de los vertebrados. En el caso particular de los seres humanos, aunque también poseen cierto grado de habilidad regenerativa, esta está mucho más limitado.
Invertebrados
El considerado miembro más primitivo de los gusanos planos o platelmintos, la planaria, es uno de los animales con mayor capacidad regenerativa. Cuando se la corta horizontalmente en varios fragmentos, cada uno de ellos es capaz de regenerar un animal completo. De la región anterior del fragmento se originaría la cabeza y de la posterior emergería la porción caudal. Por esto se plantea que la planaria tiene una capacidad regenerativa bidireccional. Por otra parte, se ha señalado que cada segmento individualizado tiene el potencial necesario para formar un gusano completo, porque en él existen células madre totipotenciales.
Las células totipotenciales poseen la capacidad de poder dar origen a millones de células, tejidos, órganos, hasta incluso embriones. Son por tanto células sin especialización.
Son muy utilizadas en cultivos in vitro para tratamientos médicos tales como la leucemia, tumores, entre otros y también en la clonación. Dicha característica la posee la mórula, de la cual luego de la blastulación comienza a dar origen a nuevas células con distintas funciones ya especificadas.
Las esponjas también pueden reconstituir su cuerpo completo a partir de pequeños conglomerados de sus propias células. Desde hace tiempo se conoce que si una esponja se fragmenta y se disocia en una suspensión de células separadas, estas después se van uniendo progresivamente hasta llegar a reconstruir el individuo completo. Otra muestra de su gran capacidad regenerativa se muestra si pasamos a uno de estos poríferos por un tamizador, cada uno de los pedazos resultantes acaba dando lugar a una nueva esponja.
Entre los equinodermos se distingue la estrella de mar, atendiendo a su gran capacidad de regeneración, ya que si pierde uno a más de sus brazos, los vuelven a regenerar con gran facilidad. En la mayoría de las ocasiones, el nuevo brazo presenta un aspecto similar al brazo perdido, pero otras veces sus características son dismórficas. Mientras que en el sitio lesionado se desarrolla progresivamente un nuevo brazo, también en el brazo desprendido del disco central de la estrella, ocurre un proceso regenerativo que da lugar a un organismo completo al conformarse el resto del animal: el disco central y los otros 4 brazos. Sobre la base de estas características, la capacidad regenerativa de la estrella de mar puede clasificarse también como bidireccional. 
Los cangrejos poseen la capacidad de realizar la autoamputación de sus extremidades en algunas situaciones de peligro. Este proceso se efectúa mediante un mecanismo reflejo denominado autonomía. Estos cangrejos tienen una articulación “destructible” cerca de la base de cada una de sus extremidades. En caso de necesidad, el animal puede romper instantáneamente la articulación para separar la extremidad de su cuerpo, sin que esto le represente un daño mayor, pues después puede regenerar el miembro desprendido. Otra propiedad regenerativa que posee es la de cambiar periódicamente su exoesqueleto para poder llevar a cabo su crecimiento y desarrollo.
De forma similar se comportan las langostas, que también expresan este mecanismo de autonomía y capacidad regenerativa de algunas partes de su cuerpo como son las pinzas, las patas y las antenas.
Vertebrados
En estos animales, especialmente en los mamíferos, se ha perdido al menos de una forma significativa, la potencialidad regenerativa de la mayor parte de sus tejidos y órganos. Por lo tanto, en ellos, un traumatismo o herida produce generalmente un daño permanente que puede ir desde una simple cicatriz hasta un grado de incapacidad habitualmente proporcional a la lesión sufrida.
Sin embargo, algunos vertebrados han retenido la habilidad regenerativa que les permite la reparación de algunos sitios dañados, e incluso la regeneración de partes perdidas, tal como se observa en invertebrados. Entre los vertebrados con estas características se destacan los peces teleósteos, los urodelos (salamandras y tritones) y otros tipos de anfibios.
Los peces pueden regenerar casi todas las partes de su sistema nervioso central, incluyendo al nervio óptico. Esta propiedad, que está bien establecida en los peces jóvenes, también se ha comprobado en los peces adultos, que pueden regenerar el nervio óptico, parte de la retina, del tallo cerebral y probablemente todos los axones de la médula espinal. Otras partes que los peces pueden regenerar son las aletas. Se ha sugerido que la amputación de una aleta provoca en los tejidos vecinos una proliferación de células epiteliales que migran hacia la zona lesionada y contribuyen a la regeneración de la parte perdida. Las escamas también pueden ser regeneradas.
Los tiburones pueden regenerar los dientes desprendidos. Es más, también tienen la capacidad de reproducir cada dos semanas su dentadura completa.
Los urodelos (salamandras y tritones) tienen una extraordinaria capacidad regenerativa, pues en cualquier momento de su vida pueden regenerar extremidades que han perdido. Pero la propiedad regenerativa no se limita en ellos a la reconstrucción de nuevas extremidades, pues se ha señalado que son los únicos vertebrados adultos que pueden regenerar también otras estructuras de su cuerpo como son los maxilares inferior y superior, los dientes, componentes oculares como el iris, el cristalino y la retina, y además parte del tejido cardíaco. Después de la amputación de una pata, la epidermis cubre rápidamente el sitio de la lesión y produce allí una estructura que se ha denominado cresta apical epidérmica, donde se forma una masa de células indiferenciadas llamada blastema, que da origen a la nueva extremidad. Se plantea que al mismo tiempo, ocurre la activación de homeogenes (como el Hox A y Hox B) en forma similar como ocurre durante el período embrionario para formar las extremidades.
Si en estos animales se elimina el cristalino, este se regenera progresivamente en el curso de varias semanas. Se ha planteado que esto es posible debido a que las células pigmentadas presentes en el diafragma del iris, pierden el pigmento, se reincorporan al ciclo celular y posteriormente se transforman en células con capacidad regenerativa del cristalino.
En las aves la capacidad regenerativa está limitada a la “muda” de su plumaje.
Los ciervos pueden regenerar sus astas fracturadas y en el ciervo común se produce anualmente un recambio de su cornamenta.
En el ser humano se expresan solo algunos procesos regenerativos, entre los que se encuentran los recambios periódicos de las células epidérmicas, de la mucosa oral y del tracto respiratorio. Las células sanguíneas mantienen un proceso continuo de destrucción y regeneración, lo que se efectúa en un tiempo que varía de acuerdo con el tipo de célula. También mantiene crecimiento del pelo y de las uñas, que continúa después de su corte. En común con otros mamíferos tiene también la capacidad de regeneración de tejido muscular cuando la lesión no ha sido extensa y la reconstrucción y consolidación de fracturas óseas. Desde hace mucho tiempo, se conoce la capacidad regenerativa de las células hepáticas y también de la piel para cerrar heridas, aunque en ella pueda quedar una cicatriz dependiendo de la magnitud de la lesión infringida.
Conclusión
A medida que el hombre ha ido adquiriendo mayores conocimientos sobre la regeneración biológica en los animales, se ha ido incrementando su interés por crear en el ser humano una capacidad regenerativa similar a la que tienen algunos animales para lograr la restauración de órganos y tejidos dañados.
Las investigaciones relativamente recientes sobre la biología celular y los nuevos conocimientos sobre las células madre, entre las que se destacan las existentes en la médula ósea, para convertirse en células de diferentes tejidos, han abierto una nueva era en la denominada medicina regenerativa, en la que ya se esta avanzando mucho sobre la materia.
Pero a medida que ahonda la investigación en este campo, aparecen confrontaciones éticas y morales sobre la posible utilización de células embrionarias sin especializar (blástulas) para conseguir la regeneración de tejidos y órganos . ¿Se les puede considerar seres vivos a un grupo de células sin especializar (y por tanto un asesinato modificarlas) o bien podríamos considerarlas unos futuros tejidos en beneficio de un ser humano que necesite de ellos?
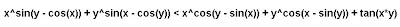que divide el plano en regiones -de las que la propia curva queda incluida como borde de una de ellas- y coloreando adecuadamente por fin conseguimos estos biomorfos:
