
¿No es increíble la fórmula de Euler? No es de extrañar que en cierta ocasión el matemático Benjamin Peirce les dijese a sus alumnos: "Caballeros, esto es sin duda cierto, es absolutamente paradójico, no podemos comprenderlo y no sabemos lo que significa, pero lo hemos demostrado y, por lo tanto, sabemos que debe ser verdad". (Epsilones)
En efecto; desarrolando en serie las funciones exponencial, seno y coseno obtendremos las expresiones:
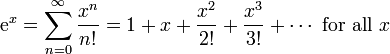


y sustituyendo x (variable real) por iz (variable compleja) llegamos a la conclusión fundamental:

es decir (siendo x un valor Real e i la unidad imaginaria)

Puesto que

y

se deduce que:
y reordenando obtenemos la identidad de Euler:



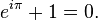


No hay comentarios:
Publicar un comentario